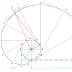
Problem 3.5 Engineering Curves – Construct an Archemedian spiral for one and half convolution. The greatest and the least radii being 50 mm and 14 mm respectively. Draw tangent and normal to the spiral at a point 40 mm from the center.
Step-1 Draw a horizontal axis of the length equal to 100 mm. And mark the center point O on it.
Step-2 Draw a vertical axis bisecting and perpendicular to the horizontal axis passing through the point O.
Step-3 With O as center and radii equal to 50 mm and 14 mm respectively draw two circles.
Step-4 Divide these circles into 12 equal divisions. And give the notations 0, 1,2,3, etc. up to 18 because of one and half convolution of the curve as shown into the figure.
Note: You can give notations in any direction either in clockwise or anticlockwise.
Step-5 Now divide the distance between the two circles, which is 50 mm – 14 mm = 36mm, on the horizontal axis into the same number of division as of the circle, which is 18 because of one and half convolution. So, the distance between the two consecutive divisions is 2 mm.
Step-6 With O as center and radius equal to O1 on the horizontal axis draw an arc between the respective divisional lines of the circle OO & O1 as per the figure given above. Like in the same way draw 18 arcs.
Step-7 Draw a smooth medium dark free hand curve from the end points of the previously drawn arcs in sequence to get Archimedian Curve.
Step-8 To draw normal and tangent to the curve mark a point say K to the curve at the given distance which is 40 mm form the center O by a compass. Draw a line starting from this point K to the center of the circle O. With this line KO draw a perpendicular line of the length equal to value of the formula given below:
X = Distance between the two radius vectors in mm/ Difference of these two radius vectors in radians.
Here it is selected as OO – O3, which is equal to 3.81 mm. Now from the end point of this line draw a medium dark line which passes through the point K, that is normal to the curve. And draw a perpendicular line to the normal and passing through the point K which is tangent to the curve.
Step-9 Give the dimensions by any one method of dimensions and give the name of the components by leader lines wherever necessary.
 |
| Click on it to zoom Procedure: |
Step-2 Draw a vertical axis bisecting and perpendicular to the horizontal axis passing through the point O.
Step-3 With O as center and radii equal to 50 mm and 14 mm respectively draw two circles.
Step-4 Divide these circles into 12 equal divisions. And give the notations 0, 1,2,3, etc. up to 18 because of one and half convolution of the curve as shown into the figure.
Note: You can give notations in any direction either in clockwise or anticlockwise.
Step-5 Now divide the distance between the two circles, which is 50 mm – 14 mm = 36mm, on the horizontal axis into the same number of division as of the circle, which is 18 because of one and half convolution. So, the distance between the two consecutive divisions is 2 mm.
Step-6 With O as center and radius equal to O1 on the horizontal axis draw an arc between the respective divisional lines of the circle OO & O1 as per the figure given above. Like in the same way draw 18 arcs.
Step-7 Draw a smooth medium dark free hand curve from the end points of the previously drawn arcs in sequence to get Archimedian Curve.
Step-8 To draw normal and tangent to the curve mark a point say K to the curve at the given distance which is 40 mm form the center O by a compass. Draw a line starting from this point K to the center of the circle O. With this line KO draw a perpendicular line of the length equal to value of the formula given below:
X = Distance between the two radius vectors in mm/ Difference of these two radius vectors in radians.
Here it is selected as OO – O3, which is equal to 3.81 mm. Now from the end point of this line draw a medium dark line which passes through the point K, that is normal to the curve. And draw a perpendicular line to the normal and passing through the point K which is tangent to the curve.
Step-9 Give the dimensions by any one method of dimensions and give the name of the components by leader lines wherever necessary.



No comments:
Post a Comment